Poissonova distribuce: Předpovězte počet gólů i vítěze utkání
Vysvětlení Poissonovi distribuce
Pissonova distribuce je matematický koncept pro převedení celkových průměrů do pravděpodobností pro různé výsledky. Tak například, Chelsea v průměru může dát 1,7 gólu na zápas. Vložíme-li tento údaj do vzorce Poissonovi distribuce, zjistíme, že Chelsea v 18,3% případů vstřelí 0 branek, v 31% případů 1 branku, ve 26,4% případů 2 branky a v 15% případů 3 branky.
Jak za pomoci Poissonovi distribuce vypočítat výsledek zápasu?
Předtím než Poissonovu distribuci budeme moci využít k výpočtu pravděpodobného výsledku zápasu, musíme vypočítat průměrný počet gólů, který každý z týmů v zápasu pravděpodobně vstřelí. Na to lze přijít za pomoci určení útočné a obranné síly obou týmů a jejich porovnání.
Při výpočtu útočných a obranných sil je velmi důležitá volba reprezentativního rozsahu dat – příliš mnoho výsledků a data nebudou pro aktuální sílu relevantní, zatímco příliš málo výsledků povede k překroucení získaných dat. Pro tuto analýzu jsme použili zápasy ze začátku sezóny 2016/17.
Výpočet útočné a obranné síly
Vypočteme průměrný počet gólů vstřelených doma a venku.
To spočítáte tak, že celkový počet gólů vstřelených v minulé sezóně vydělíte počtem odehraných zápasů:
Celkový počet gólů, které tým vstřelil doma (za celou sezónu)/Počet zápasů
Celkový počet gólů, které tým vstřelil venku (za celou sezónu)/Počet zápasů
V sezóně 2015/16 anglické Premier League padlo 567/380 gólů na domácí půdě a 459/380 na cizím hřišti, což znamená průměrně 1,492 gólů na zápas na domácím hřišti a 1,207 gólů na zápas na cizím hřišti.
- Průměrný počet gólů vstřelených na domácím hřišti: 1,492
- Průměrný počet gólů vstřelených na cizím hřišti: 1,207
Rozdíl od výše uvedeného průměru nám udává „útočnou sílu“.
Vedle toho budeme potřebovat také průměrný počet gólů, který průměrný tým Premier League obdrží. Tuto hodnotu dostaneme jednoduše tak, že výsledky výše obrátíme.
- Průměrný počet gólů, který tým dostal na domácím hřišti: 1,207
- Průměrný počet gólů, který tým dostal na cizím hřišti: 1,492
Nyní získaná čísla výše můžeme použít pro výpočet útočné a obranné síly Evertonu a Tottenhamu pro zápas, který byl plánován na 16. srpna 2014.
Předpověď výsledku pro Tottenham
Výpočet útočné síly Tottenham Hotspur:
- Krok 1: Vezmeme počet gólů, vstřelených minulou sezónu na domácím hřišti (Tottenham: 35), a vydělíme jej počtem zápasů odehraných na domácím hřišti (35/19): 1,842.
- Krok 2: Vydělíme toto číslo průměrným počtem gólů na jeden zápas na domácím hřišti za sezónu (1,842/1,492). Výsledkem je „útočná síla“ 1,235.
- (35÷19) ÷ (567÷380) = 1,235
Výpočet obranné síly Evertonu:
- Krok 1: Vezmeme počet gólů, který tým hrající na cizím hřišti minulou sezónu na cizích hřištích dostal (Everton: 25), a vydělíme jej počtem zápasů odehraných na cizím hřišti (25/19): 1,315.
- Krok 2: Vydělíme toto číslo průměrným počtem gólů, které dostaly týmy hrající na cizím hřišti na jeden zápas za sezónu (1,315/1,492). Výsledkem je „obranná síla“ 0,881.
- (25÷19) ÷ (567÷380) = 0,881
Nyní můžeme použít následující vzorec pro výpočet pravděpodobného počtu gólů vstřelených domácím týmem:
Góly vstřelené Tottenham Hotspurs = útočná síla Tottenhamu × obranná síla Evertonu × průměrný počet gólů.
V tomto případě to je 1,235 × 0,881 × 1,492 = 1,623, čímž se dopracujeme k tomu, že Tottenham vstřelí 1,683 gólu.
Předpověď výsledku pro Everton
Výpočet útočné síly Evertonu: (24÷19) ÷ (459÷380) = 1,046
Výpočet obranné síly Tottenhamu: (15÷19) ÷ (459÷380) = 0,653
Nyní můžeme použít následující vzorec pro výpočet počtu branek, které by mohl vstřelit hostující tým:
Tím se dostaneme k výpočtu 1,046 × 0,653 × 1,207 = 0,824
Poissonova distribuce při sázení – předvídání výsledků utkání
Samozřejmě že žádná hra neskončí výsledkem 1,623 ku 0,824 – jedná se prostě o průměr. Poissonova distribuce, vzorec vytvořený francouzským matematikem Simeonem Denisem Poissonem umožňuje použít tyto údaje k výpočtu pravděpodobností v celé řadě zápasů. Možnosti jsou uvedeny v následující tabulce:
Samotný vzorec vypadá takto: P(x; μ) = (e-μ) (μx) / x!
Nicméně abyste se nezdržovali, můžete použít online nástroje (Poissonova kalkulačka) určené právě pro výpočet Poissonovi rovnice.
Vše, co musíte udělat, tak je zadat různé gólové výsledky (0-5) v náhodné proměnné (x) kategorii a pravděpodobnost skórování týmu (například Tottenham 1,623) v průměrné míře úspěšnosti a kalkulátor už všechno zařídí.
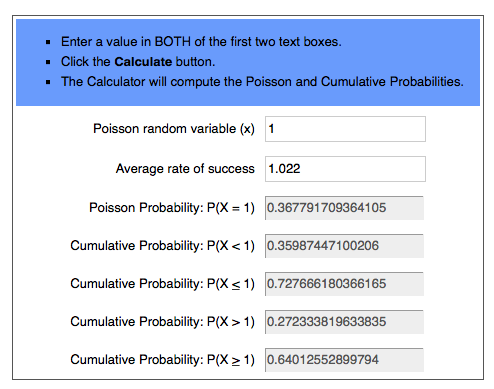
Poissonova distribuce pro Manchester United vs. Swansea City
| Góly | 0 | 1 | 2 | 3 | 4 | 5 |
| Tottenham | 19,73% | 32,02% | 25,99% | 14,06% | 5,07% | 1,85% |
| Everton | 43,86% | 36,14% | 14,89% | 4,09% | 0,84% | 0,14% |
Tento příklad ukazuje, že je 19,73% šance, že Tottenham nedá žádný gól, 32,02% šance na jeden gól Tottenhamu a 25,99% šance, že tento tým dá góly dva. Everton naproti tomu má 43,86% pravděpodobnost nulového skóre, 36,14% šanci na jeden gól a 14,89% na dva góly. Doufáte, že jeden z týmů dá pět gólů? U Tottenhamu máte šanci 1,85 % a u Evertonu 0,14 %.
Protože oba výsledky jsou (z matematického pohledu) nezávislé, vidíte, že očekávaný výsledek je 1:0. Pokud obě pravděpodobnosti vynásobíte, získáte pravděpodobnost výsledku 1:0 – 0,1404 čili 14,04 %.
Když nyní víte, jak vypočítat pravděpodobnost výsledků, můžete svá zjištění porovnat s kurzy v sázkové kanceláři a zjistit, zda najdete rozdíly, kterých byste mohli využít.
Příklad: Porovnání remízy
Čtěte také strategie sázení, které jsou oblíbené u ostatních čtenářů!
Výše uvedený příklad nám ukázal, že podle našeho modelu má remíza 1:1 11,53% šanci na výskyt. Ale co kdybychom raději vsadili na „remízu“, nežli na konkrétní skóre? V takovém případě byste měli vypočítat pravděpodobnost všech různých remíz – tedy 0 – 0, 1 – 1, 2 – 2, 3 – 3, 4 – 4, 5 – 5 atd.
To uděláte jednoduše tak, že vypočítáte pravděpodobnost všech možných kombinací remízy a dáte je dohromady. To vám dá šanci na výskyt remízy, bez ohledu na skóre.
Samozřejmě že existuje nekonečný počet možností remízy (tak například oba týmy mohou za zápas vstřelit 10 gólů), nicméně šance na remízu vyšší jak 5 – 5 je tak malá, že je docela bezpečné je z tohoto modelu úplně vynechat.
V zápasu United – Swansea by byla šance na remízu 0,266 nebo 26,6%. Pokud byste na tuto příležitost dostali například kurz 5,530, dostanete se k implicitní pravděpodobnosti 18,08%.
To znamená, že pokud by forma z minulé sezóny perfektně ukazovala výsledky v sezóně aktuální a navíc skutečně byly tak vysoké kurzy, sázka by se nám hodně vyplatila. Bohužel určit hodnotu sázky není vždycky tak jednoduché, jak to vypadá. Poissonova analýza má i svá omezení.
Limity Poissonovy distribuce
Poissonova distribuce je jednoduchý model pro předpovídání, který nebere v potaz hromadu důležitých faktorů. Nezohledňuje situační faktory – jako jsou novinky v klubu, herní postavení atd. – a subjektivní analýzy každého týmu během přestupové pauzy.
V tomto případě by byla opomíjena skutečnost, že Manchester United do zápasu vstupoval s novým manažerem Louisem Van Gaalem, což by byla vcelku chyba.
Ignorovány jsou i různé další vlivy jako například vliv daného hřiště, které počet gólů může významně ovlivnit.
Výhodu nad bookmakery sázkařům dávají především zápasy v nižších ligách. V hlavních ligách je opravdu těžké tento náskok získat. Sázkové kanceláře totiž zaměstnávají lidi s odbornými znalostmi. Pokud chcete být před nimi, vedle Poissonovy analýzy doporučujeme získat i další znalosti.
Zdroj: Pinnacle Sports
Můžete se podělit s jinými čtenáři níže














































Vydělíme tuto hodnotu průměrným počtem gólů vstřelených týmem hostů za zápas (1,474/1,574) abychom získali „obrannou sílu : 0,936. To nás dovede ke skutečnosti, že Swansea vstřelí o 6,35% méně gólů nežli „průměrný“ tým Premier League.nnnPřece nemůžu počítat obranou sílu swansea tím že počítám kolik dají gólů venku to je nesmysl, obranná síla je snad o tom kolik gólů obdržím ne ?
Dobrý den, jedná se pouze o mezisoučet, kt. vychází ze vzorečku počtu vstřelených gólů. Procentuální šance na obdržené góly se tak vlastně vůbec nepočítají.
ale jo, u toho prvniho vypoctu je chyba.nU "Výpočet obranné síly Swansea City: se pocita s poctem vstrelenych golu Swansea" – tam ma byt pocet obdrzenych golu Swansea venkunprotoze U "Výpočet obranné síly Manchesteru United:" se pocita s poctem obdrzenych golu Manchesteru – takze jedno nebo druhy musi byt spatne nebo to nedava smysl. nJak jsem rekl vyse – Ja si myslim, ze to prvni je spatne…
Dobrý den, spíš se jednalo o trošku nešťastný překlad. Teď je vše opraveno, mělo by to již být správně. Omlouvám se.
Dobrý den,npřijde mi, že ve výpočtu je chyba už v zadání. Jednou je uvedeno, že Swansea dala venku 28 gólů (viz Předpověď výsledku pro Manchester United) a pak jen 21 gólů (viz Předpověď výsledku pro Swansea City). Ať to počítám jak počítám, tak ke stejnému výsledku jako vy dojít nemůžu.nMám pravdu, nebo jen něco přehlížím? Můžete prosím upravit výpočet?nDíky.
Dobrý den, máte pravdu. Zdroj, z kterého byl článek převzatý, byl chybný. Článek byl překopaný podle jiného zdroje. Teď by měl být už skutečně dobře. Děkujeme za vaši trpělivost, vážíme si vašeho zájmu. Pro příště se vynasnažíme takových nešťastných článků vyvarovat. Hezký den.
LadyAmbiente: Děkuju za rychlou úpravu článku! Nyní vše dává smysl. Jen pár překlepů: Výpočet útočné síly Tottenham Hotspur, bod 3 by měl být "(35÷19) ÷ (569÷380) = 1,235" a data jsou platné pro začátek sezóny 2016/2017, ne k srpnu 2014. A samozřejmě obrázek je platný k původnímu článku pro porovnání Manchasteru se Swansea.
Ja pouzivam poissonovu distribuciu na pravdepodobnost 2 golov a viac ale hlavne na stavku ze oba timy daju gol. Je to velmi dobra pomocka na urcenie pravdepodobnosti tychto dvoch udalosti.
ja velka pomucka to je na 2 a více golů?Tato sazka je moje oblibena
Dobrý den, je tato metoda se zahrnutim vypoctu prumeru cele ligy přesnější? Četl jsem i o poissonove distribuci, kde to bylo takto: utocna sila tymu+obrana sila týmu÷2= nějaké číslo.
Dobrý den, Poissonova distribuce je velmi dobrou pomůckou i při sázení na 2 a více gólů.
Myslel jsem si, že tomu rozumím a používám to správně, ale když se podívám, že například při výpočtu počtů gólů domácích použiji nejdříve jejich průměrný počet gólů na zápas, který vydělím průměrným počtem gólů na zápas v celé lize a pak to vynásobím s tímtéž, ale obdrženým počtem hostů, tak pak nechápu, proč to zase násobíme průměrným počtem gólů v lize. V příkladu: "Krok 2: Vydělíme toto číslo průměrným počtem gólů na jeden zápas na domácím hřišti za sezónu (1,842/1,492). Výsledkem je „útočná síla“ 1,235." Jenže my to pak opět násobíme tím 1,492 a dojdeme k 1,842 a pak to násobíme s obranou silou soupeře… proč tedy nenásobit jen průměrný počet daných gólů domácích s obranou silou hostů?
Dobrej postřeh. Celý to nedává úplně smysl a v článku jsou i chyby ve výpočtech.
Dobrý den, chyby byly již opraveny.
Musím uznat, že mě článek velmi zaujal, ale nechápu proč se do výpočtu zahrnuje celá liga a nepočítá se pouze s konkrétními soupeři a tím pádem by mě zajímalo, jak by vypadal výpočet v takovém případě.
Jde o to, že při počítání pouze vzájemných zápasů byste měl jen velmi malý vzorek – týmy se v sezóně potkají 2x, přes léto se pak často významně mění kvůli přestupům. Poissonova distribuce však pracuje takovým způsobem, že porovnává aktuální sílu všech týmů, tzn. že každý zápas by měl mít vypovídací hodnotu i k síle daných týmů. Každý tým má pak nějaké skóre, přičemž toto skóre se patřičným způsobem odráží na skóre týmu, který ho porazil/vyhrál nad ním. Snad je to dostatečně srozumitelné. Pokud ne, klidně se ptejte dál. 🙂
Dobrý den, pokud jsou opraveny, prosím o vysvětlení níže uvedených údajů.n- …V sezóně 2015/16 anglické Premier League padlo 567/380 gólů na domácí půdě…n 3. (35÷19) ÷ (569÷380) = 1,235n 3. (25÷19) ÷ (564÷380) = 0,886nproč se ve výpočtech liší počty vstřelených gólů? Nejdříve je to 567, poté 569, 564…nn- 1,235 × 0,881 × 1,492 = 1,683. Výsledek je špatně, vychází na 1,623.nn- …Samozřejmě že žádná hra neskončí výsledkem 1,4631 ku 0,824…n jak jste dospěli k číslu 1,4631?nnPředem děkuji
Dobrý den, máte pravdu. Článek byl převzatý z doposud velmi důvěryhodného zdroje, tudíž jsme se spolehli na to, že údaje byly správné. Po první urgenci jsme článek opět opravili podle zdroje, který během té doby také provedl úpravy. Nicméně jak vidíte, ani to nepomohlo. Nyní jsme článek upravili již podle nás. Takto by to mělo být skutečně správně. Děkujeme vám za váš čas a ochotu nás upozornit na chyby a nedostatky, také díky tomu se náš web neustále rozvíjí.
Zdravím, tento článek je velmi zajímavý a podnětný, a proto bych se chtěl zeptat, zda to někdo zkoušel a jaké jsou případně vaše zkušenosti.