Úskalí sázkového systému Martingale
Někteří sázkaři hodně spoléhají na sázkové strategie, ale jsou skutečně tak spolehlivé, jak se jeví? Podívali jsme se do hloubky na sázkový systém Martingale a prozkoumali jsme, zdali výnosy skutečně stojí za riziko, které přináší.
Existují sázkaři, kteří money management sázkové systémy jako například Martingale (zvýšení sázky poté, co prohrajeme, ve snaze vyhrát dříve prohrané peníze) obhajují. Vycházejí přitom z toho, že jednou výhra přijít musí, přičemž vyhrají všechny dříve prohrané peníze zpět a ještě navíc získají zpočátku vytyčený profit.
Všímavější sázkaři si již všimli jednoho velkého problému – v hazardních hrách výhra není nevyhnutelná. Jinými slovy řečeno, výhra nikdy nemusí přijít. Kdyby výhra nevyhnutelná byla, tak by se nejednalo o hazard. Důvod, proč někteří sázkaři tento základní nedostatek ignorují, vychází z obvyklých předsudků – přehnané důvěry, že skutečně vyhraje a podcenění pravděpodobnosti ztrátových sérií. Tento druh money managementu je známý pod tradičním názvem Martingale.
Strategie Martingale
Sázková strategie Martingale pochází ze světa kasinových her a to zejména z rulety. Na ruletě je značně populární sázení na červenou-černou, kdy hráč prostě rozhoduje, zda míček po spinu přistane na červené nebo černé barvě.
Budeme-li přehlížet výhodu kasina (house-edge), potom jsou šance na výhru přesně 2,00. Myšlenka základní Martingale strategie přitom je, zdvojnásobit svou sázku vždy, jakmile prohrajete. Jakmile zaznamenáte výhru (a tudíž získáte zpět své peníze a to včetně dříve vytyčeného zisku), vrátíte se k výchozí sázce. Avšak stejně dobře můžete aplikovat tento vzorec:
Míra progrese Martingale = kurz/(kurz – 1)
Takže například, pokud jsou sázkové kurzy 3,00, míra progrese zvýšení sázky by měla být 1,5 (sázka po prohraném spinu tedy nebude navýšena 2×, ale pouze 1,5×).
Tímto způsobem jsou po každé výhře vynulovány předchozí ztráty plus se dostanete k vytyčenému zisku (více v následující sekvenci točení na ruletě).
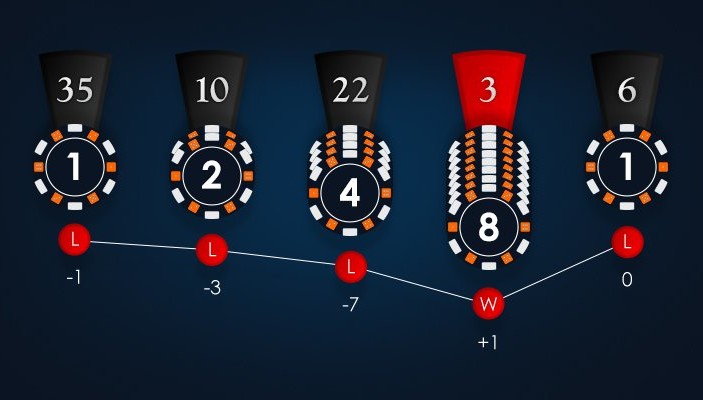
| Spin | Sázka | Velikost sázky | Výsledek | Výhra/prohra | Profit | Profit celkem |
|---|---|---|---|---|---|---|
| 1 | Červená | 1 | Černá | Prohra | -1 | -1 |
| 2 | Červená | 2 | Černá | Prohra | -2 | -3 |
| 3 | Červená | 4 | Černá | Prohra | -4 | -7 |
| 4 | Červená | 8 | Červená | Výhra | +8 | +1 |
| 5 | Červená | 1 | Černá | Prohra | -1 | 0 |
| 6 | Červená | 2 | Červená | Výhra | +2 | +2 |
| 7 | Červená | 1 | Červená | Výhra | +1 | +3 |
| 8 | Červená | 1 | Černá | Prohra | -1 | +2 |
| 9 | Červená | 2 | Černá | Prohra | -2 | 0 |
| 10 | Červená | 4 | Červená | Výhra | +4 | +4 |
Martingale změní riziko, nikoliv matematické očekávání
Stuart Holland ve své e-knize Successful Staking Strategies (2001) ukázal jednoduchou, ale velmi zajímavou ukázku toho, proč Martingale nedokáže udělat NĚCO z NIČEHO.
Vezměme si první tři spiny, které jsme uvedli v tabulce výše. Tyto 3 po sobě jdoucí prohry (vytočení černé barvy) představují ve své podstatě pouze jeden z osmi možných výsledků, z nichž je každý stejně pravděpodobný, jako všechny ostatní.
Níže uvedená tabulka ukazuje, že ziskové očekávání pro každou z těchto 8 permutací, kde R = červená a B = černá, snižuje vliv house edge (výhody kasina) v podobě zelené nuly. Pro výpočet očekávání jakéhokoliv výsledku stačí jednoduše vynásobit aktuální profit nebo ztrátu pro tento výsledek a to pravděpodobností jeho výskytu.
| Permutace | Sázka | Výsledek | Výška sázky | Profit | Celkem | Změna | Očekávání |
|---|---|---|---|---|---|---|---|
| 1 | R, R, R | B, B, B | 1, 2, 4 | -1, -2, -4 | -7 | 0,125 | -0,875 |
| 2 | R, R, R | B, B, R | 1, 2, 4 | -1, -2, +4 | +1 | 0,125 | +0,125 |
| 3 | R, R, R | B, R, B | 1, 2, 1 | -1, +2, -1 | 0 | 0,125 | 0 |
| 4 | R, R, R | B, R, R | 1, 2, 1 | -1, +2, +1 | +2 | 0,125 | +0,25 |
| 5 | R, R, R | R, B, B | 1, 1, 2 | +1, -1, -2 | -2 | 0,125 | -0,25 |
| 6 | R, R, R | R, B, R | 1, 1, 2 | +1, -1, +2 | +2 | 0,125 | +0,25 |
| 7 | R, R, R | R, R, B | 1, 1, 1 | +1, +1, -1 | +1 | 0,125 | +0,125 |
| 8 | R, R, R | R, R, R | 1, 1, 1 | +1, +1, +1 | +3 | 0,125 | +0,375 |
Shrnutí jednotlivých očekávání pro všech osm permutací nám dává celkové očekávání pro tuto strategii. Je jím nula. Z toho důvodu můžeme při hraní rulety z dlouhodobého hlediska doufat tak maximálně v to, že zůstaneme na nule. Očekávat, že v dlouhodobém horizontu nad ruletou vyhrajeme, je scestné.
Ve skutečnosti se ovšem nedostaneme ke spravedlivé ruletě – jediná hra na červenou-černou nabízí negativní očekávání – abychom mohli mluvit o „spravedlivé ruletě“, museli bychom zahrnout opravdu velkou spoustu her.
Podobná analýzy velikosti sázky (kde jsou všechny sázky o stejné hodnotě) přichází se stejným výsledkem – celkové očekávání je nula.
| Permutace | Sázka | Výsledek | Výška sázky | Profit | Celkem | Změna | Očekávání |
|---|---|---|---|---|---|---|---|
| 1 | R, R, R | B, B, B | 1, 1, 1 | -1, -1, -1 | -3 | 0,125 | -0,375 |
| 2 | R, R, R | B, B, R | 1, 1, 1 | -1, -1, +1 | -1 | 0,125 | -0,125 |
| 3 | R, R, R | B, R, B | 1, 1, 1 | -1, +1, -1 | -1 | 0,125 | -0,125 |
| 4 | R, R, R | B, R, R | 1, 1, 1 | -1, +1, +1 | +1 | 0,125 | +0,125 |
| 5 | R, R, R | R, B, B | 1, 1, 1 | +1, -1, -1 | -1 | 0,125 | -0,125 |
| 6 | R, R, R | R, B, R | 1, 1, 1 | +1, -1, +1 | +1 | 0,125 | +0,125 |
| 7 | R, R, R | R, R, B | 1, 1, 1 | +1, +1, -1 | +1 | 0,125 | +0,125 |
| 8 | R, R, R | R, R, R | 1, 1, 1 | +1, +1, +1 | +3 | 0,125 | +0,375 |
Pojďme se na tyto dvě tabulky podívat blíže. Sázková strategie Martingale zvýší počet případů, kdy můžeme očekávat výhry (profit), alespoň v porovnání se strategií sázení z individuální hry, v tomto případě ze 4 na 5.
Bohužel to je na úkor jedné velké ztráty. Vše, co Martingale ve skutečnost dokáže, je změna v rozložení rizik. Snaha o získání jednoho výsledku s pozitivním očekáváním navíc přináší mnohem větší negativní očekávání, vztahující se na ekvivalent výsledku pro úroveň sázek. To je zdroj vlastního nebezpečí, který je s touto strategií neodmyslitelně spojený.
Zdroj: Pinnacle Sports
Máte názor k zápasu? Můžete se podělit s jinými čtenáři níže
Zatím bez komentáře
Sázkové kanceláře
Jak na sázení
Rubriky
Top autoři
Poměr výher: 73.5 %
Poměr výher: 73.5 %
Poměr výher: 62.3 %
Top zápasy